백준 1922: 네트워크 연결(Java)

문제링크 : https://www.acmicpc.net/problem/1922

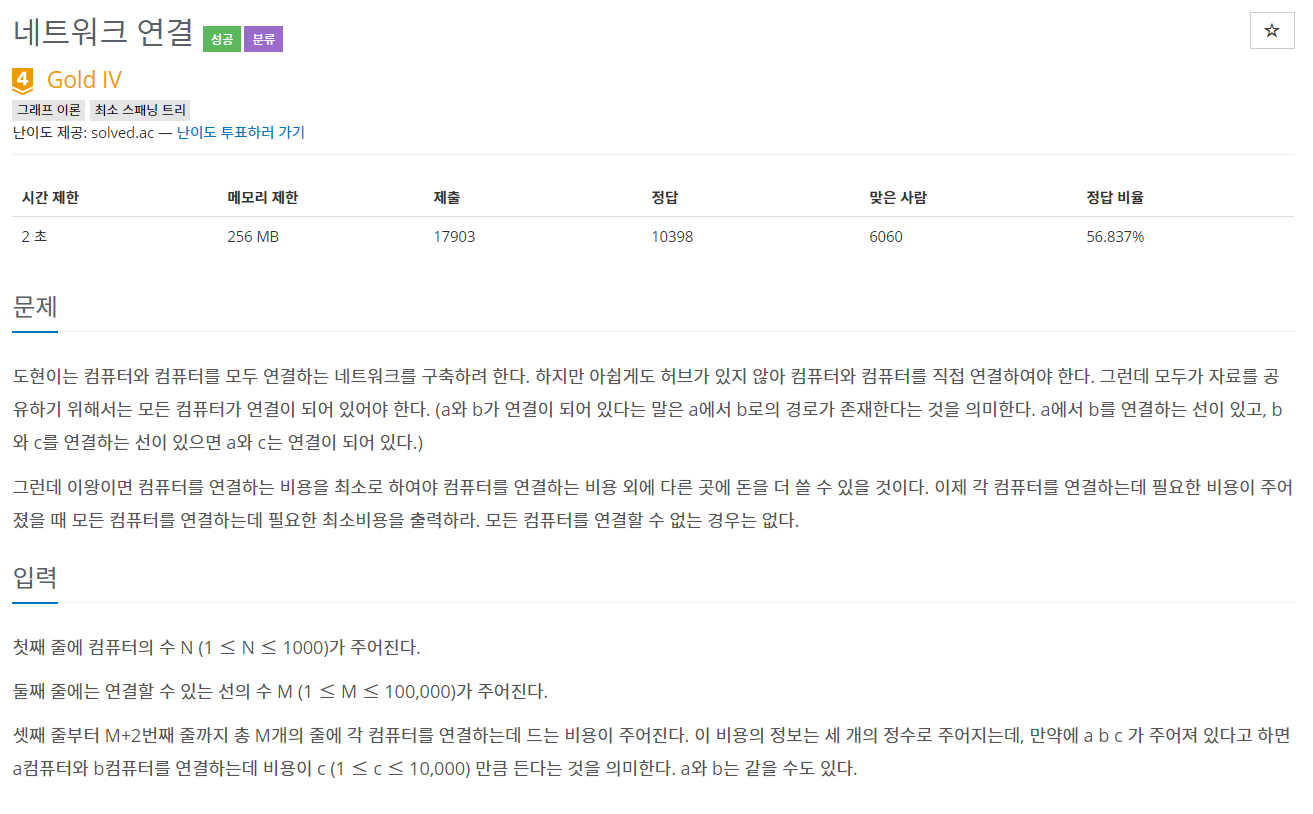
문제

문제를 해결한 방법

최소 스패닝 트리(MST) 문제로 최소 비용으로 모든 정점을 연결해야합니다.

MST 문제는 Kruskal 알고리즘 과 Prim 알고리즘 2가지로 풀이할 수 있는데 구현방식에 차이가 있습니다.

Kruskal

1. 모든 간선들의 가중치를 오름차 순으로 정렬
2. 가중치가 가장 작은 간선을 선택
3. 위에서 선택한 간선이 연결하려는 2개의 정점이 서로 연결되지 않은 상태라면, 2개의 정점을 서로 연결한다.
4. 이 과정을 반복

Prim

1. 임의의 정점을 선택
2. 선택한 간선의 정점으로부터 가장 낮은 가중치를 갖는 정점을 선택
3. 모든 정점이 선택될 때까지 반복

Kruskal vs Prim

• Kruskal은 간선 위주의 알고리즘, Prim은 정점 위주의 알고리즘
• Prim의 경우 최소 거리의 정점을 찾는 부분에서 자료구조의 성능에 영향을 받는다.
• Kruskal은 간선을 기준으로 정렬하는 과정이 오래 걸린다.

따라서, 간선의 개수가 작은 경우에는 Kruskal 알고리즘, 간선의 개수가 많은 경우에는 Prim 알고리즘이 적합하다.

소스 코드(Kruskal)

package baek;

import java.io.*;
import java.util.*;

public class Main_1922_네트워크연결_kruskal {
	public static int[] parent;
	public static int N,M;
	public static ArrayList<int[]> graph;
	
	public static int getParent(int num) {
		if(parent[num] == num)
			return num;
		
		return getParent(parent[num]);
	}
	
	public static void union(int a, int b) {
		int computerA = getParent(a);
		int computerB = getParent(b);
		
		if(computerA == computerB) return;
		
		if(computerA > computerB)
			parent[computerA] = computerB;
		else
			parent[computerB] = computerA;
	}
	
	
	public static int kruskal() {
		int sum = 0;
		for(int i=0;i<graph.size();i++) {
			int[] curr = graph.get(i);
			
			if(getParent(curr[0]) != getParent(curr[1])) {
				sum += curr[2];
				union(curr[0], curr[1]);
			}
		}
		return sum;
	}
	

	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		M = Integer.parseInt(br.readLine());
		
		parent = new int[N+1];
		graph = new ArrayList<int[]>();
		
		for(int i=1;i<=N;i++)
			parent[i] = i;
		
		for(int i=0;i<M;i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			int from = Integer.parseInt(st.nextToken());
			int to = Integer.parseInt(st.nextToken());
			int value = Integer.parseInt(st.nextToken());
			
			graph.add(new int[] {from,to,value});
		}
		
		Collections.sort(graph, new Comparator<int[]>() {
			
			@Override
			public int compare(int[] a, int[] b) {
				return Integer.compare(a[2], b[2]);
			}
		});
		
		System.out.println(kruskal());
	}
}

소스 코드(Prim)

package baek;

import java.io.*;
import java.util.*;

public class Main_1922_네트워크연결_prim {
	static ArrayList<int[]>[] graph;
	static int N,M;
	
	public static int prim() {
		int sum = 0;
		boolean[] visit = new boolean[N+1];
		
		PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
			@Override
			public int compare(int[] o1, int[] o2) {
				return Integer.compare(o1[1], o2[1]);
			}
		});
		
		pq.add(new int[] {1,0});
		
		while(!pq.isEmpty()) {
			int[] curr = pq.poll();
			
			if(visit[curr[0]]) continue;
			
			visit[curr[0]] = true;
			sum += curr[1];
			
			for(int i=0;i < graph[curr[0]].size();i++) {
				int[] next = graph[curr[0]].get(i);
				
				if(visit[next[0]]) continue;
				
				pq.add(next);
			}
		}
		
		return sum;
	}
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		M = Integer.parseInt(br.readLine());
		
		graph = new ArrayList[N+1];
		
		for(int i=1;i<=N;i++)
			graph[i] = new ArrayList<int[]>();
		
		for(int i=0;i<M;i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			int from = Integer.parseInt(st.nextToken());
			int to = Integer.parseInt(st.nextToken());
			int value = Integer.parseInt(st.nextToken());
			
			graph[from].add(new int[] {to,value});
			graph[to].add(new int[] {from,value});
		}
		
		System.out.println(prim());
	}
}